Integrando datos provenientes de distintas técnicas “ómicas”

En un experimento de secuenciación por bisulfito, una observación se refiere a cada posición en la secuencia genómica en la cual se ha determinado su grado/estado de metilación (se puede utilizar una escala discreta, continua o categórica). En un experimento de RNA-Seq, cada observación se refiere a las cuentas de una secuencia específica (en general un transcrito) y en un experimento de genotipificación cada observación se refiere a una variante genética. Usualmente a estas observaciones se les llama features o dimensiones y es frecuente que en el contexto de técnicas "ómicas" su número vaya desde miles a millones por experimento. Para facilitar la visualización e interpretación de estas observaciones, se suele generar una representación de los datos utilizando dos o tres dimensiones. Estas dimensiones se les puede llamar latentes por el hecho de que no son evidentes y deben definirse. Algunas técnicas de reducción de dimensiones comúnmente utilizadas son PCA, t-SNE y UMAP. En general, se busca que esta representación de las observaciones utilizando un número (mucho) menor de dimensiones, “capture” una parte relevante de la heterogeneidad biológica observada entre las distintas condiciones experimentales o fenotipos estudiados. Esta última idea es compartida por otro tipo de análisis llamado Factor Analysis, donde se definen factores que no son directamente observados, latentes, que además de ayudar a la visualización e interpretación de nuestros datos como lo hacen otras técnicas de reducción de dimensiones, definen nuevos módulos funcionales. Idealmente, se espera que estos módulos ayuden a explicar en algún grado las diferencias biológicas existentes entre las condiciones experimentales o fenotipos.

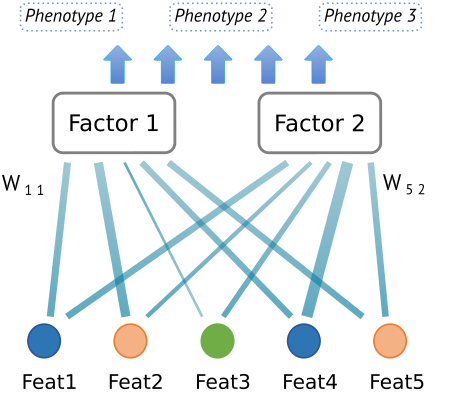
En el esquema superior, se presentan 5 observaciones que están relacionados con 2 factores latentes a través de pesos (W), donde el grosor de las líneas representa una mayor o menor importancia de cada feature sobre cada factor. El color de los features representa mediciones que provienen desde diferentes técnicas (RNA-Seq, genotipificación, etc.). Estos factores latentes pueden interpretarse como módulos que tienen el potencial de agregar información adicional a la información proveniente del análisis de cada modalidad por separado.

Multiple factor analysis con MOFA y MOFA2

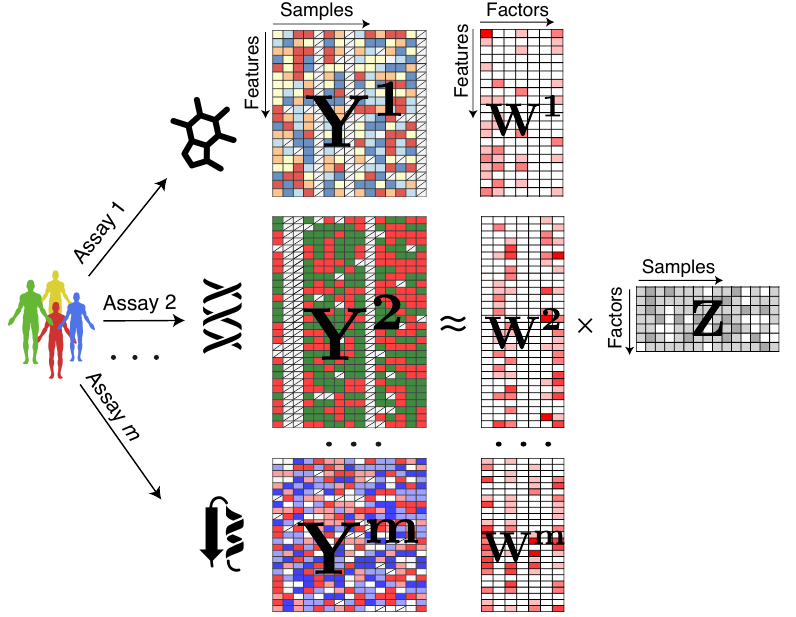
Multiple Factor Analysis se refiere al caso particular donde se integran datos provenientes desde diversas técnicas experimentales, donde cada técnica genera una “modalidad de datos”. Un ejemplo de este tipo de análisis es ”Multi-Omics Factor Analysis”, implementado en las librerías MOFA y su sucesor MOFA2. En el siguiente esquema, se representa la factorización de matrices llevada a cabo por MOFA, donde los datos introducidos son presentados por las matrices \(Y\) (input, una por cada modalidad de datos). MOFA descompone estos inputs en matrices de pesos (weights), una por modalidad de datos, y una matriz de factores, común a todas las matrices \(Y\), donde cada factor tiene tantos elementos como el número de muestras. Si bien este esquema es presentado en la publicación que introduce MOFA, representa una metodología general de factorización de matrices en el contexto de factor analysis.

Los resultados pueden analizarse de múltiples formas, donde la descomposición de la varianza explicada por cada uno de los factores en cada modalidad de datos es un paso central en este análisis.

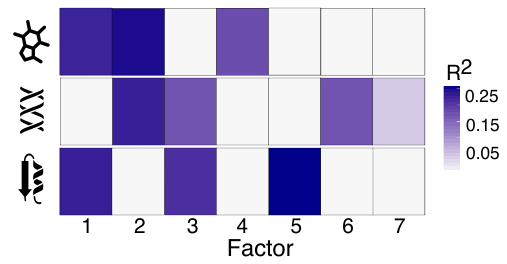
Cada factor en MOFA puede estar definido por el aporte de múltiples modalidades de datos, aunque el modelo que implementa permite que haya features con peso 0, lo que se traduce en un modelo con menos variables explicativas y por ende tiene el potencial de ser un modelo más interpretable. De esta forma, MOFA no solo permite definir la variabilidad compartida entre modalidades de datos, sino que también la variabilidad única a una modalidad específica de datos. El objetivo general del análisis de estos factores es tratar de entender cómo estos se relacionan con sus pesos y como estos pueden ayudar a explicar los diferentes fenotipos observados.

Los datos utilizados para generar las visualizaciones son presentados en esta publicación y fueron descargados desde acá. En la publicación se generó un modelo utilizando la librería MOFA, mientras que aquí se utiliza MOFA2 (ver más adelante algunas diferencias). Mi intención no es explicar los resultados de una publicación particular, sino que tratar de ilustrar como funciona MOFA y factor analysis de una forma general y relativamente breve.

Factores

Cada uno de los factores definidos por MOFA captura las diferencias entre muestras y son análogos a los “componentes principales” definidos en PCA, donde cada “componente principal” se refiere a un eje que captura la mayor variabilidad posible entre los datos cuando estos son proyectados sobre este eje. Aquí, cada factor ordena las muestras/células sobre un eje centrado en 0, donde signos opuestos manifiestan fenotipos opuestos. Por ejemplo, si un factor captura parte de variabilidad asociada con el ciclo celular, células/muestras en mitosis deberían presentarse cercanas a un extremo (no importa el signo), mientras que células en G1 deberían estar cercanas al extremo opuesto, con células de fenotipos intermedios más cercanas a 0. En el estudio, células fueron extraídas desde embriones de ratón en diferentes días de desarrollo y fueron sometidas a ensayos de RNA-Seq, grado de metilación y accesibilidad a la cromatina. Los gráficos aquí presentados provienen de un análisis realizado con MOFA2, utilizando alrededor de 800 células extraídas en el día 7.5. Cada factor esta presentado por 840 puntos donde cada punto es una célula que esta coloreada según su valor de factor (eje \(Y\)).

Una de las tantas formas de explorar los factores es graficándolos unos contra otros y utilizar información anexa a los experimentos (metadata). En este caso en particular, los factores 1 y 2 capturan las diferencias entre capas germinales.

Pesos (weights/loadings)

Los gráficos anteriores por sí solos no dan información sobre qué features estarían afectando los fenotipos capturados por cada factor. Para eso es necesario explorar los pesos presentes en cada modalidad de datos (views en la jerga interna de MOFA). En cada modalidad, cada feature tiene asociado un peso (arriba, ver primera figura), un valor numérico que da muestra de su importancia en cada factor. Si un feature tiene un peso positivo quiere decir que tendrá niveles más altos en las muestras que tienen valores positivos de factor y viceversa, donde su valor absoluto indica la importancia que tiene en dicho factor. En general es recomendable explorar el aporte de los features de cada modalidad sobre cada factor. Aquí se presentan los pesos de cada observación proveniente desde RNA-Seq sobre el factor 1.

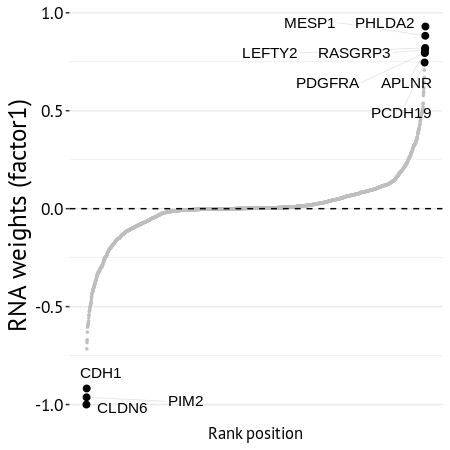
El grafico contiene 2500 puntos, que es el número de transcritos que pasaron filtros de control de calidad. El valor absoluto de cada punto determina la “fuerza” que tiene cada feature y se muestran los 10 mayores pesos. Sus valores han sido escalados entre –1 y 1. La posición en el eje X, su ranking, no es importante. Se muestran los nombres de los 10 genes con mayor peso en el factor 1. Una vez obtenidos los features top de cada modalidad de datos, es posible llevar a cabo cualquier tipo de análisis que pudiese realizarse con una lista de genes/mutaciones/etc., e.g. estudiar si alguna ruta metabólica o algún tipo ontológico esta especialmente representado en dicha lista, realizar un análisis de redes, entre otros.

Requisitos para usar MOFA

Número de réplicas:

No es necesario tener datos provenientes desde experimentos single-cell pero si se requiere que haya al menos 15-20 muestras, lo que lo hace en la práctica compatible con pocos estudios que analizan datos de grupos de células (bulk).

Datos de diversas modalidades:

Si bien la definición general de una modalidad de datos se refiere a datos provenientes desde un tipo particular de técnica experimental, no es necesario que sea así y cada modalidad/view puede definirse según el contexto del estudio. Por ejemplo, desde datos de metilación y acceso a DNA (solo dos técnicas experimentales), pueden definirse views según la naturaleza funcional de la secuencia sobre la cual se encuentra la observación, e.g. enhancers lejanos o cercanos, promotores, etc. También puntos temporales y localizaciones físicas diferentes (secuencias extraídas de diferentes órganos, etc.) pueden servir como views en MOFA. En un estudio de microbiomas, cada view puede definirse según alguna categoría taxonómica relevante de la cual provienen las secuencias.

Otras aplicaciones de MOFA

Al igual que otros tipos de factorización de matrices como PCA o “Non-Negative Matrix Factorization” (este último grupo de algoritmos es relativamente popular en librerías que implementan alguna versión de Factor analysis, e.g. cNMF y CoGAPS ), MOFA captura relaciones lineales entre features. Aun así, los factores obtenidos pueden ser directamente utilizados como input en técnicas como tSNE o UMAP, que pueden capturar relaciones no lineales entre observaciones (ver figura 3 en publicación):

Adicionalmente, los factores encontrados por MOFA pueden ser utilizados en modelos predictivos de relevancia en clínica. Por ejemplo, en el contexto de estudios sobre tratamientos de enfermedades, los factores pueden ser utilizados como covariables en un modelo de sobrevivencia u otro tipo modelo acorde, donde es posible analizar la importancia de determinados factores latentes en la respuesta al tratamiento.

Sobre el modelo estadístico en MOFA

MOFA/MOFA+ implementan un modelo estadístico basado en Bayesian Group Factor Analysis. Se basa específicamente de ideas procedentes de Variational Bayes. MOFA define factores, variables no observadas (latentes) y su objetivo es obtener la distribución posterior de estas variables latentes (los factores, \(X\)) dadas las observaciones (\(Y\)):

Donde el denominador no tiene una solución definida. Así, en inferencia variacional se aproxima la distribución \(p(X|Y)\) con una distribución más simple (distribución variacional). Esta distribución más simple se busca dentro de una familia de distribuciones que si pueden calcularse y el problema pasa a ser el definir esta familia de distribuciones y posteriormente encontrar esta distribución variacional. La función objetivo que MOFA optimiza (en este caso maximiza), se conoce como Evidence Lower Bound, ELBO, que tiene una relación definida con una métrica de similitud entre distribuciones (KL-divergence). Así, al maximizar la función ELBO se minimiza la diferencia entre este grupo de distribuciones conocidas y la distribución real.

MOFA y MOFA2 pueden utilizar múltiples modelos de likelihood dependiendo de la modalidad de datos del input. Las distribuciones disponibles son de Gauss, Bernoulli y binomial, pero por motivos de eficiencia computacional y robustez, los autores recomiendan transformar el input a variables continuas de ser posible y así utilizar un modelo gaussiano. Por ejemplo, para datos de RNA-Seq se puede utilizar una función como vst en DESeq2 y para datos de grados de metilación, se puede realizar una conversión a M-values aplicando una transformación logit.

En general, en Factor analysis se debe definir el número de factores que se espera encontrar, lo que no es necesariamente trivial. MOFA2 automáticamente eliminará factores que no explican un porcentaje de varianza mínimo (que es susceptible de ser cambiado por el usuario). A priori, no es fácil determinar qué porcentaje de varianza debe explicar un factor para ser considerado útil, pues dependiendo del estudio, factores que explican varianzas tan bajas como 1% pueden ser biológicamente interpretables. Siempre es posible eliminar los factores que explican el menor porcentaje de varianza de forma posterior al training del modelo, esto dependiendo del “poder explicativo” que puedan brindar al estudio.

En MOFA, se sugiere probar diferentes inicializaciones del modelo y posteriormente analizar la consistencia de los factores encontrados en cada una de las instancias del modelo. En MOFA2 esto no es necesario. La inicialización del modelo parte desde los componentes principales obtenidos de todos los datos concatenados (las matrices \(Y\) en el esquema), haciendo innecesario entrenar el modelo múltiples veces (ver material complementario en MOFA+).

Implementación de MOFA y MOFA2

En MOFA y MOFA2 el modelo estadístico esta implementado en python y las funciones para analizar los resultados están implementadas en R. En el caso de MOFA2, opcionalmente, se puede utilizar GPUs (procesadores gráficos/ “tarjetas de video”) si estos son compatibles con CUDA, haciendo mucho más rápida la creación/training del modelo. Como referencia, entrenar un modelo con 15 views, donde cada view tiene 800 muestras y 1000 features o más, fue 3 veces más rápido en un GPU que un CPU (300 versus 1300 segundos, 1070GT vs 6 cores 2019). Para esto, MOFA2 usa cupy, una librería que implementa múltiples operaciones existentes en numpy siguiendo una notación igual o similar a este, pero utilizando CUDA internamente, simplificando la tarea de escribir código compatible con GPU y CPU a la vez. Aquí, un pequeño extracto desde el repositorio de MOFA2:

# Se pueden definir funciones que implementan operaciones básicas
# entre matrices y utilizar CUDA si está disponible:
import numpy as np
import  cupy as cp
...
def exp(mat):
    if gpu_mode:
        return cp.exp(mat)
    else:
        return np.exp(mat)
...